回顧前一篇

昨天有跟著做的人可能會發現，怎麼寫出來的程式沒有畫面 XDD

可能經過一番掙扎後，才發現需要多加了一行 camera.position.z = 5 恰好為今天埋下伏筆！

順道一提，像這種時候，若不確定是不是語法的錯誤，可以右鍵進入瀏覽器「檢測」，點選「主控台」可以得到錯誤提示訊息。或是直接鍵盤 F12 按下去！

import './style.css'
import * as THREE from 'three'

const scene = new THREE.Scene()
scene.background = new THREE.Color('salmon')

const aspectRatio = window.innerWidth / window.innerHeight
const camera = new THREE.OrthographicCamera(-aspectRatio * 5, aspectRatio * 5, 5, -5, 0.1, 1000)

const renderer = new THREE.WebGLRenderer()
renderer.setSize(window.innerWidth, window.innerHeight)
document.body.appendChild(renderer.domElement)

const geometry = new THREE.ConeGeometry()
const material = new THREE.MeshBasicMaterial({ color: 0x00ff00 })
const cube = new THREE.Mesh(geometry, material)
scene.add(cube)

camera.position.z = 5

renderer.render(scene, camera)

那昨天的範例大概如上，透過有點弧度的圓錐體，可以輕鬆看到 perspective camera 和 orthographic camera 的差別，還請大家玩玩看唷。

說好的動畫呢？

「完成了第一個 Hello, World! 程式固然開心，但只有一個模型，頂多移動一些角度，實在是很無趣，我用純 CSS 都可以做更有趣、更酷的東西⋯⋯」

我聽到你的心聲了！馬上來介紹今天的重頭戲——讓我們的方塊動起來！

首先，先要了解動畫是如何運作、以及如何在網頁上運作的。我們都知道電影、電視、甚至遊戲裡的動畫是由許多幀數的畫面在短時間內快速播放以達到動畫的效果，瀏覽器內也是一樣。一般來說遊戲的動畫會希望可以達到 60 FPS (frame per second)，以達到足夠流暢的畫面跟即時的反應，但又不會把電腦燒起來的平衡。我們之後會討論如何監測這個需求。

回到瀏覽器，因為每台電腦的效能不同，也會直接影響瀏覽器的 fps，所以如果我們把程式碼寫以 fps 來跑，比較快的電腦中的動畫就會比較快XD 這不是我們期待的結果。因此取而代之的是調用 requestAnimationFrame 來獲取 frame 的時間，透過這個時間差來知道動畫要動多少。

window.requestAnimationFrame() 方法通知瀏覽器我們想要產生動畫，並且要求瀏覽器在下次重繪畫面前呼叫特定函數更新動畫。

當準備好更新頁面上的動畫時應當呼叫這個方法。這表示向瀏覽器請求在下次重繪前呼叫這個動畫函數。回呼的次數通常落在每秒 60 次，但通常會根據 W3C 的建議符合多數瀏覽器重新整理的頻率。——〔MDN Web Docs 社群〕

最後就是要注意， requestAnimationFrame 裡需要提供一個 callback 以用於下一次重 render 的時候調用。

所以我們可以把 renderer.render(scene, camera) 改成如下，每一幀我們去旋轉方塊的 x 跟 y，然後再畫出來，就完成一個簡單的動畫了！

function animate() {
    requestAnimationFrame(animate)
    cube.rotation.x += 0.01
    cube.rotation.y += 0.01
    renderer.render(scene, camera)
}
animate()

實作

那我們來看細部的程式碼，除了上面例子的 rotation 還可以怎麼動？ rotation 本身還有沒有什麼規範與用法？

首先，先來想想看動可能的要素包含什麼？如果有用過 3D 軟體 (Blender, Unity, etc) 的人可能馬上能回答出來。

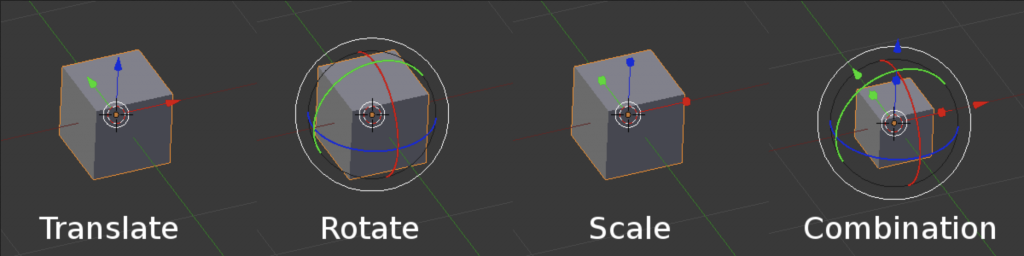
三種 transform 包含位移移動、角度轉動、大小縮放，然後可以形成許多不同的組合。這些 attributes 可以在 Object3D 裡找到，也分別就是 .position (vector3)、 .rotation (euler)、 .scale (vector3)。

Vector3

在表示位移跟縮放，Vector3 都很直觀地表達了「改變的量」，舉例來說 camera.position.z = 5 代表相機在 z 軸移動了 +5 單位

Euler

Euler 角顯示在 3D 空間中，物體在 object space 的三個軸向分別轉了幾度 (radian)，如下圖顯示。這個的好處就是非常直觀，因為我們只要根據物體的三個軸向去定義度數。

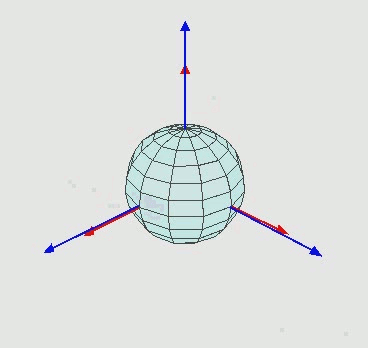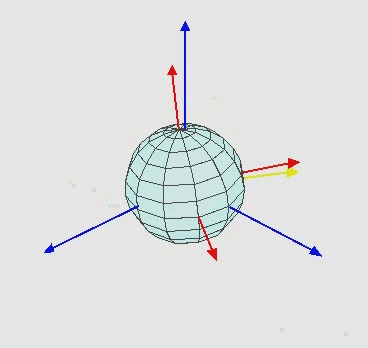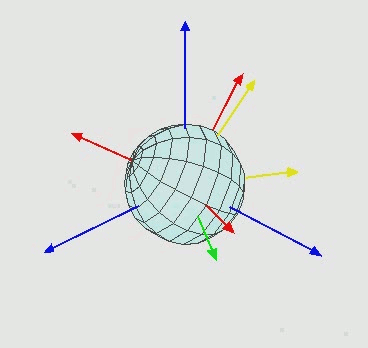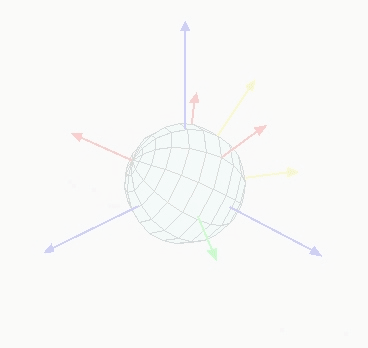
但是，這時就產生一個問題，如果沿著某一個軸轉了 90 度，那這個軸就會與另一個軸重疊。像是下圖的綠色軸與紫色軸重疊，就失去了一個自由度，這個問題叫做 Gimbal lock。

此時某個數學家跳出來，說道「沒有人是完美的、除了 quaternion！」（並沒有）

Quaternion

不知道讀者還記不記得高中曾經學過的虛數 i，我們今天不僅要來複習虛數的概念，還要介紹他的朋友——更多的虛數！

Quaternion 提供三個虛數 i, j, k，其中他們符合這些條件：

—

⋯⋯講到這裡，不知道你眼冒金星了沒，我第一次學到 quaternion 的時候整個人驚呆了，覺得數學真是帥死了！但也難死了！及至目前，我實習時候的主管、同事講到 quaternion 還是感到害怕且困惑 XDD 所以如果沒有完全理解的話也沒有關係，我們活在資訊唾手可得的時代，且讓 wikipedia 來解救。

對於i、j、k本身的幾何意義可以理解為一種旋轉，其中i旋轉代表X軸與Y軸相交平面中X軸正向向Y軸正向的旋轉，j旋轉代表Z軸與X軸相交平面中Z軸正向向X軸正向的旋轉，k旋轉代表Y軸與Z軸相交平面中Y軸正向向Z軸正向的旋轉，-i、-j、-k分別代表i、j、k旋轉的反向旋轉。——〔維基百科 四元數〕

—

Quaternion 有效率的解決 Gimbal lock 的困境，經過合理的運算也可以以 euler angle 的型態呈現，在 3D 的基本運算成了一個很好的工具，尤其感謝前人，不管是哪個 rendering library 都必定會提供這個工具，我們在此的 scope 是只要會使用即可。我們來看看 three.js 官網怎麼說。

最常用的方法有幾個，都是從各種比較好理解的 presentation 轉換成 quaternion，像是 .setFromAxisAngle 就從三個軸向想要轉的角度去生成四元數、 .setFromEuler 拿 euler 角算出四元數、 .setFromRotationMatrix 使用 3x3 的旋轉矩陣計算出 quaternion，所以不管你手邊的資料是什麼都可以輕鬆的得到四元數。

休息一下

今天提到一些概念，或許對部分人還不太能理解是什麼意思，像是 object space 是什麼？那還有其他的 space 嗎？ rotation matrix 是什麼？為什麼 rotation matrix 是 matrix4 的 upper part？

這些會在之後的章節提到，因為我覺得礙於篇幅與資訊量，可能在這邊暫停會是一個比較好的選擇。雖然今天沒有很多實作，不過所介紹的資訊，已經可以跟昨天的基本場景有很好的結合！！透過上面提供的 animate 方法，已經可以在瀏覽器中做出簡單但有一點酷酷的動畫啦 ^0^/

那麼我們就明天見！歡迎隨手按一個喜歡，謝謝！